
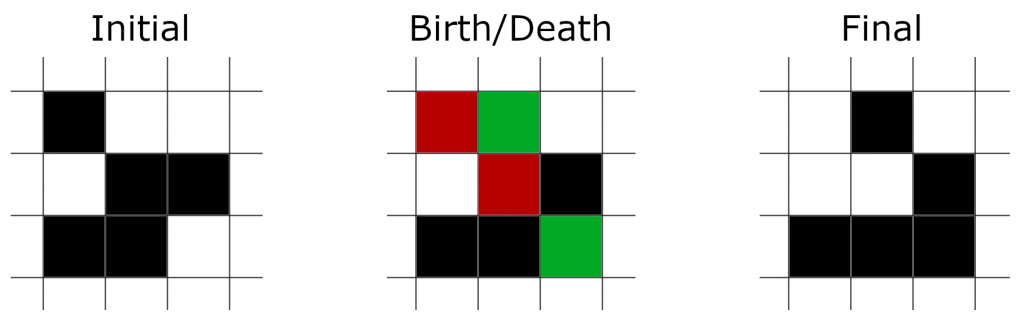
* Constructs a new Game of Life with the specified dimensions. * Data representing the grid in 1d format. * Java class for simulation of Conway's Game of Life. Any dead cell with exactly 3 neighbors comes to life.īelow is a java class which implements the Game of Life - including the grid, a random seed, and the rules:.Any live cell remains alive if it has 2 or 3 neighbors, otherwise the cell dies (as if from overcrowding or undercrouding).The rules of the Game of Life are quite simple: Although simple rules and even random seeds determine the future states of the Game of Life, unique shapes and behaviors emerge within the grid, for instance shapes which alternate states, cells (or groups of cells) which remain constant, and even groups of cells which move across the grid. Conways Game of Life is a well-known cellular automaton in which each generation of a population evolves from the previous one according to a set of. A random or predetermined state - also known as a seed - initializes the Game of Life, after which the grid is ran through several iterations, within each iteration the rules determine the state of each cell. Within this grid are cells, each of which can have two states - alive or dead. Conways Game of Life (henceforth GoL) is a deterministic cellular automaton (CA), which is binary (a cell has two possible states: 0 and 1) and runs on an. "Dyalog Webinars: APL CodeGolf Autumn Tournament".Conway's Game of Life is a simple cellular automata often represented visually in 2D space by a 2-dimensional grid. ↑ Gitte Christensen & Adám Brudzewsky.APL88 Conference Proceedings, APL Quote-Quad Vol. "Life: Nasty, Brutish, and Short" ( web). Reprinted SIGPLAN Notices Volume 7, Issue 4 in Algorithms. Reprinted SIGPLAN Notices Volume 6, Issue 10 see Front matter p. "Conway's Game "Life"", APL Quote Quad Vol. This model consists of cells arranged in a grid. This model is based on the fact that life cannot exist when there is an under or overpopulation and under the right conditions there is a chance of reproducing real life. ↑ Martin Gardner "Mathematical Games – The fantastic combinations of John Conway's new solitaire game "life"". Game of life also known as Conways game of life is a model that simulates the creation, existence, and destruction of life.Vector journal Volume 23 special supplement "Dyalog at 25". John Scholes' notes, as part of the dfns workspace, includes a more in-depth treatment.

It finds adjacent elements by rotating the original array, causing elements at the edge to wrap around (giving a torus geometry). The implementation takes advantage of nested arrays and the Outer Product to produce many copies of the argument array. More recently, it is sometimes seen as a use case for the Stencil operator, which provides a concise way to work on three-by-three neighborhoods as used by the Game of Life.Ī famous video by John Scholes explains the following Dyalog APL implementation step by step. APL implementations have appeared in the APL Quote-Quad since 1971, a year after the rules of the Game of Life were first published. Because it involves interactions between adjacent elements of the matrix, and can take advantage of APL's convenient and fast Boolean handling, implementing the Game of Life is a popular activity for APLers. The Game of Life is defined on an infinite Boolean grid, but usually only finite patterns, where all 1 values fit in a finite Boolean matrix, are studied. After the initial configuration has been. Conway's Game of Life is a well-known cellular automaton in which each generation of a population "evolves" from the previous one according to a set of predefined rules. Conways Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970.


 0 kommentar(er)
0 kommentar(er)
